TCG Card Shop Simulator: Optimal Price Guide

Discover a nerdy yet practical approach to crafting the optimal pricing strategy. Learn how rule-of-thumb approximations can guide your decision-making for maximum profitability.

TCG Card Shop Simulator: Optimal Price Guide

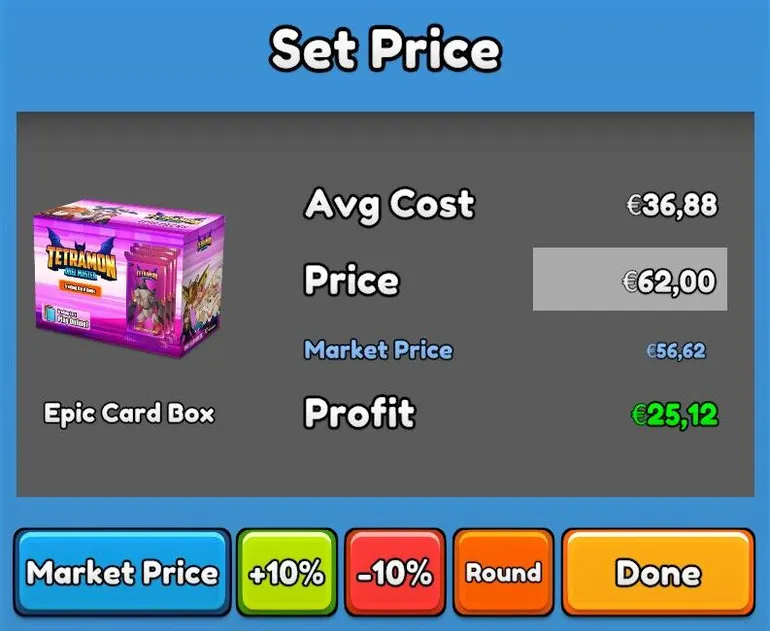
The analysis reveals that the best pricing strategy is:

1. Click on Market Price
2. Compare Profit and Avg Cost
3. If Profit > Avg Cost -> done
4. If Profit < Avg Cost -> +10% and compare Profit and Avg Cost again
5. If 2 * Profit > Avg Cost -> done
6. If 2 *Profit < Avg Cost -> +10% again (total +20%) and done

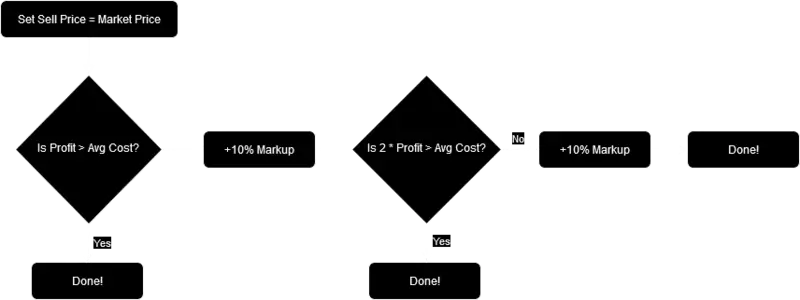
Selling below Market Price and over 30% markup is never the optimal price in terms of Profit. A markup of 30% is optimal, if Profit and Avg Cost are very close together within 10% deviation. I am not sure, if the game even allows for such a case. For completeness and without speculation about how the game determines Market Price and Avg Cost, the complete optimal pricing strategy is:

1. Click on Market Price
2. Compare Profit and Avg Cost
3. If Profit > Avg Cost -> done
4. new : If 10 * Profit < Avg Cost -> +30% and done
5. If Profit < Avg Cost -> +10% and compare Profit and Avg Cost again
6. If 2 * Profit > Avg Cost -> done
7. If 2 * Profit < Avg Cost -> +10% again (total +20%) and done

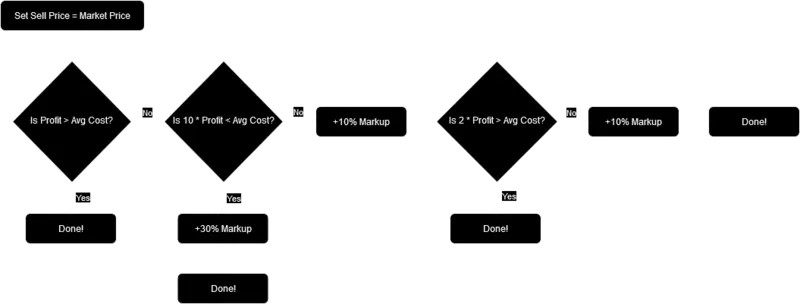
Additionally, if we do not care about +20%/+30% and only want to consider Market Price/+10%, than the strategy reduces to:

1. Click on Market Price
2. Compare Profit and Avg Cost
3. If Profit > Avg Cost -> done
4. If Profit < Avg Cost -> +10% and done

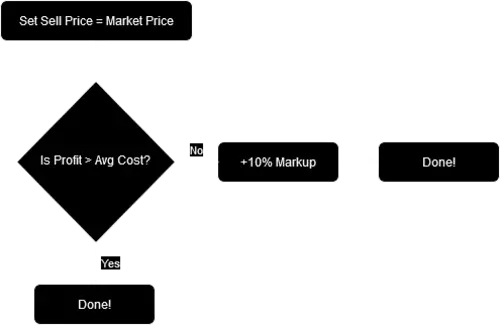
Assumptions

Sell Price Deviation from Market Price	Purchase Probability
-20%	100%
-10%	95%
0%	90%
+10%	75%
+20%	60%
+30%	45%
+40%	15%
+50%	5%
+60%	1%
>+60%	0%

Goal

We want to maximize our Profit by setting the best Sell Price. We know these two quantities relate to each other in the following way:

• Profit = Sell Price – Purchase Cost

Additionally, we need to consider the customer purchase probability p:

• Expected Profit = (Sell Price – Purchase Cost) * p

For convenience, everytime Profit is mentioned from now on, we mean Expected Profit.

Since we want to set our Sell Price in terms of deviation from the Market Price (which we call x), we need to express the Sell Price in terms of x:

• Sell Price = x * Market Price

Therefore, we want to find x such that the Profit is maximized:

• Profit = (x * Market Price – Purchase Cost) * p

Exploration

A good approach to such a problem, if we have no idea how to solve it, is to do some explorations first. We can simply try different combinations of x, Market Price, Purchase Cost and observe how the Profit changes (note that p is fixed for explicit x). We tell a computer to try out all combinations of:

• x between 0.8 and 1.6 (equivalent to -20% and +60%)
• Market Price between 0 and 100
• Purchase Cost between 0 and 100

For all combinations of Market Price and Purchase Cost, we record the x with the highest Profit. We can visualize the result in a heatmap:

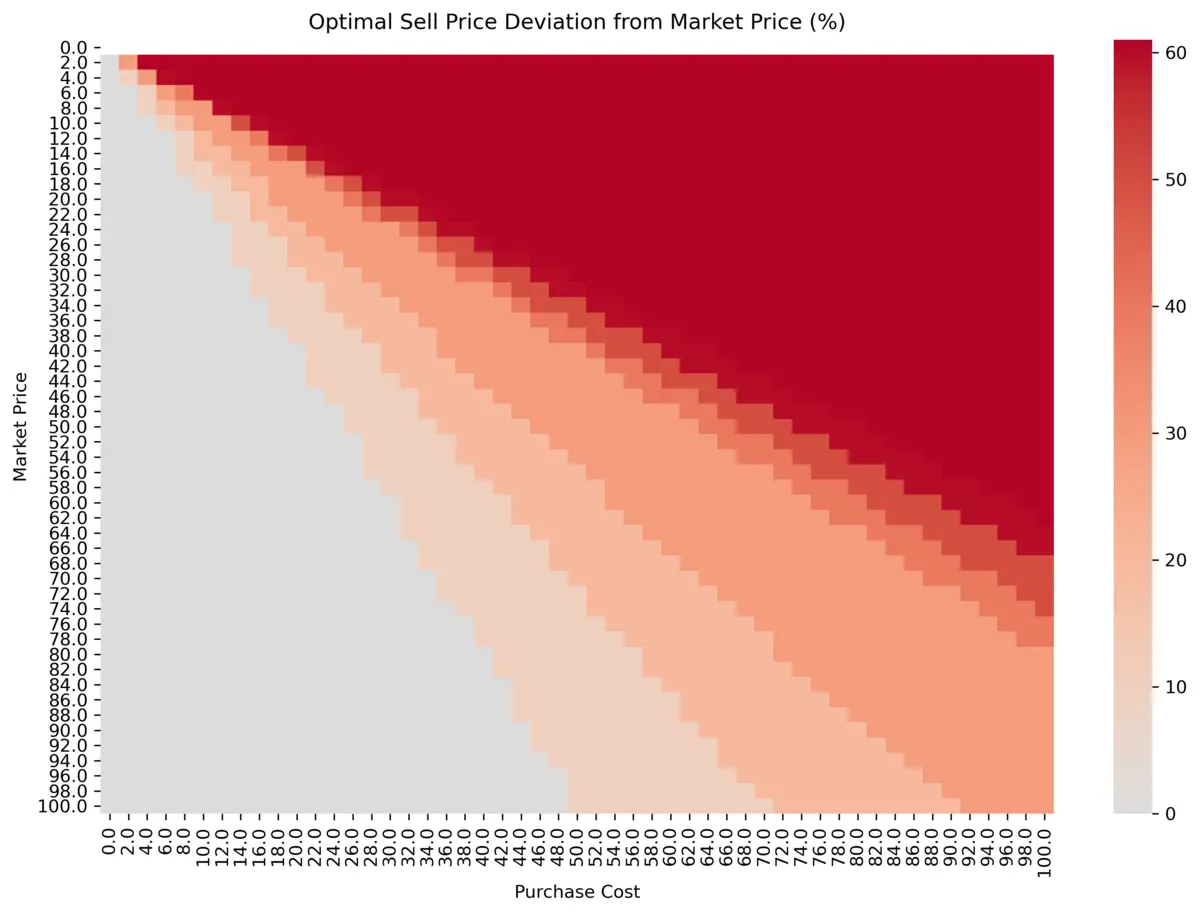
The first observation is, that it is never optimal to sell below Market Price (i.e. -20% or -10%). Second, under the reasonable assumption, that Market Price > Purchase Cost, half of the heatmap can be ignored (i.e. everything above the diagonal). Therefore, it is never optimal to sell above 30% markup (i.e. 40%, 50%, 60%, …).

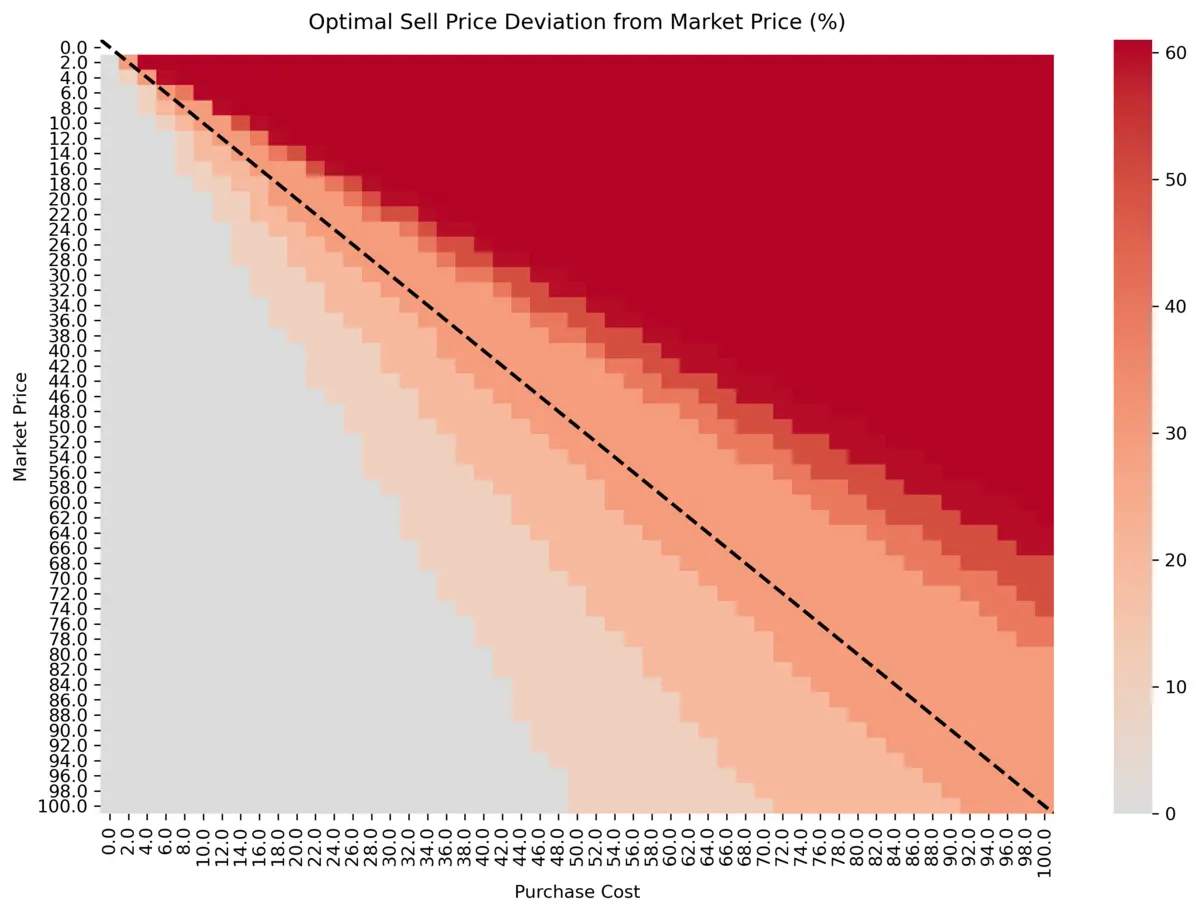
Generalized Decision Boundaries

Based on the first exploration, we concluded that the only optimal Sell Price is either at Market Price or with 10%/20%/30% markup, depending on the combination of Market Price and Purchase Cost. Now, we want to extract generalized decision boundaries, that are independent from the actual values of Market Price and Purchase Cost, which we had chosen in the exploration section. We observed from the heatmaps, that the decision boundaries are linear with positive slope and without any offset, which can be parametrized by:

• Market Price = m * Purchase Cost + b (with m>0, b=0)

Note, that the y-axis goes in the opposite direction. Using the same exporation approach as before, we can simply try different values of m and visualize it in the heatmap:

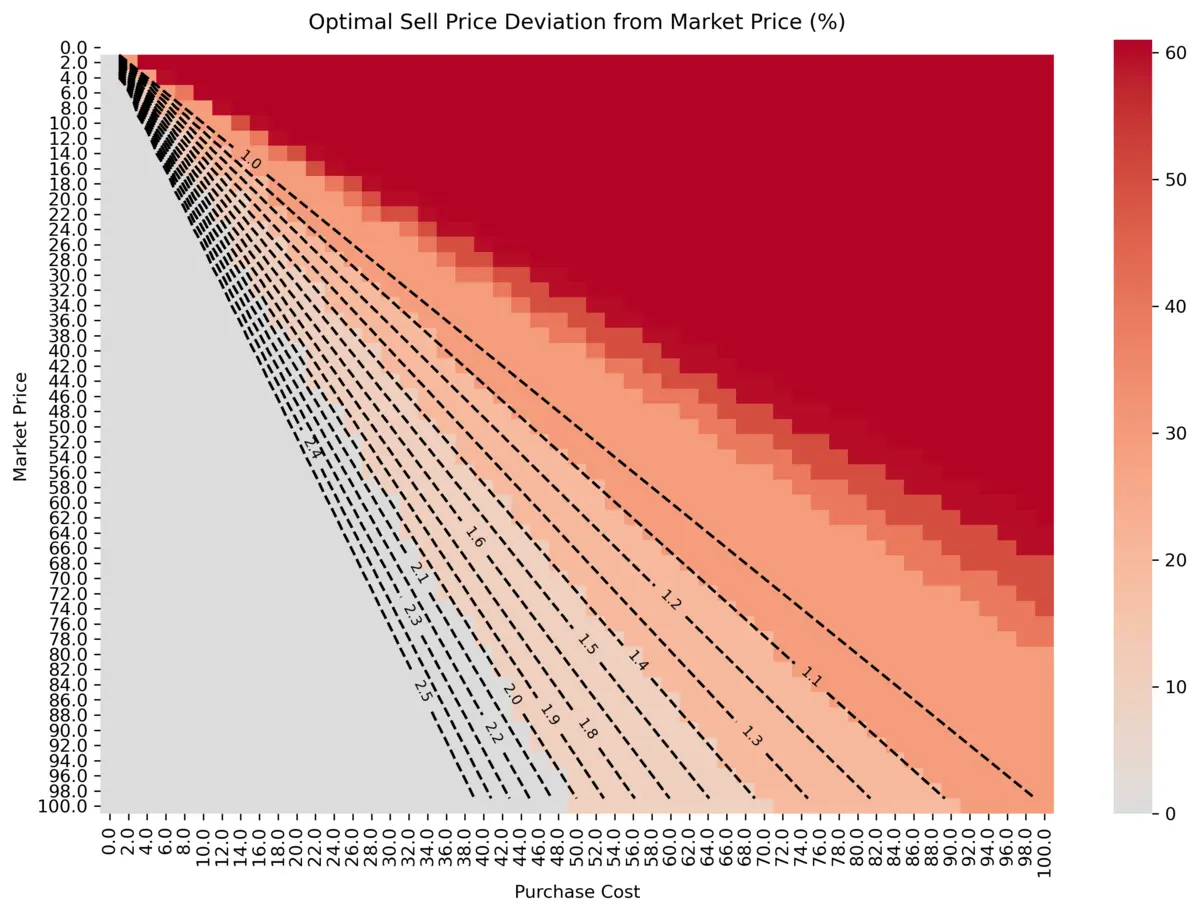
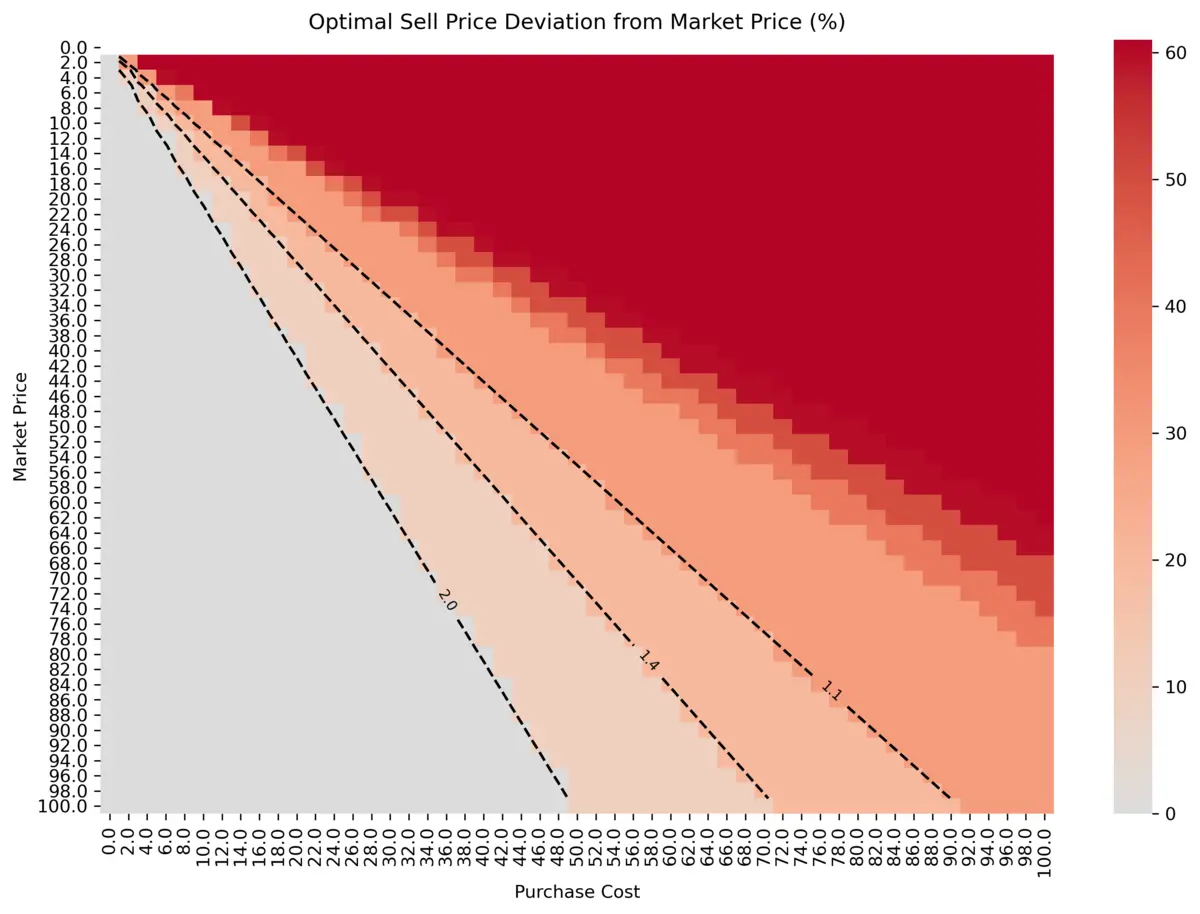
We observe, that the decision boundaries are approximately at m = 1.1, 1.4, 2.0.

Rewriting the linear function as:

• m = Market Price / Purchase Cost

We can extract conditions for optimal x, that maximizes Profit, based on the discovered decision boundaries:

1. Market Price is optimal, if Market Price / Purchase Cost > 2.0
2. +10% is optimal, if 2.0 > Market Price / Purchase Cost > 1.4
3. +20% is optimal, if 1.4 > Market Price / Purchase Cost > 1.1
4. +30% is optimal, if 1.1 > Market Price / Purchase Cost > 1.0

Deriving Practical Rule of Thumb

Note, that in this section Profit is not Expected Profit anymore, but simply (Profit = Sell Price – Purchase Cost), because the game does not show Expected Profit to the player.

Unless someone writes a mod, exactly computing Market Price / Purchase Cost ratios everytime without a calculator is not that easy. When setting the Sell Price in game, we are shown the following values: Purchase Cost, Sell Price, Market Price and Profit.

Since Profit is shown, we can rewrite the decision boundaries in terms of Profit and Purchase Cost instead. For Sell Price = Market Price , the first decision boundary becomes:

2.0 < m = Market Price / Purchase Cost = Sell Price / Purchase Cost = (Profit + Purchase Cost) / Purchase Cost = (Profit / Purchase Cost) + 1

1.0 < Profit / Purchase Cost

Purchase Cost < Profit

The decision boundary of m = 1.4 is a bit awkward to work with. We repeat the whole computation of m with deviations from 1.1 * Market Price instead of just Market Price:

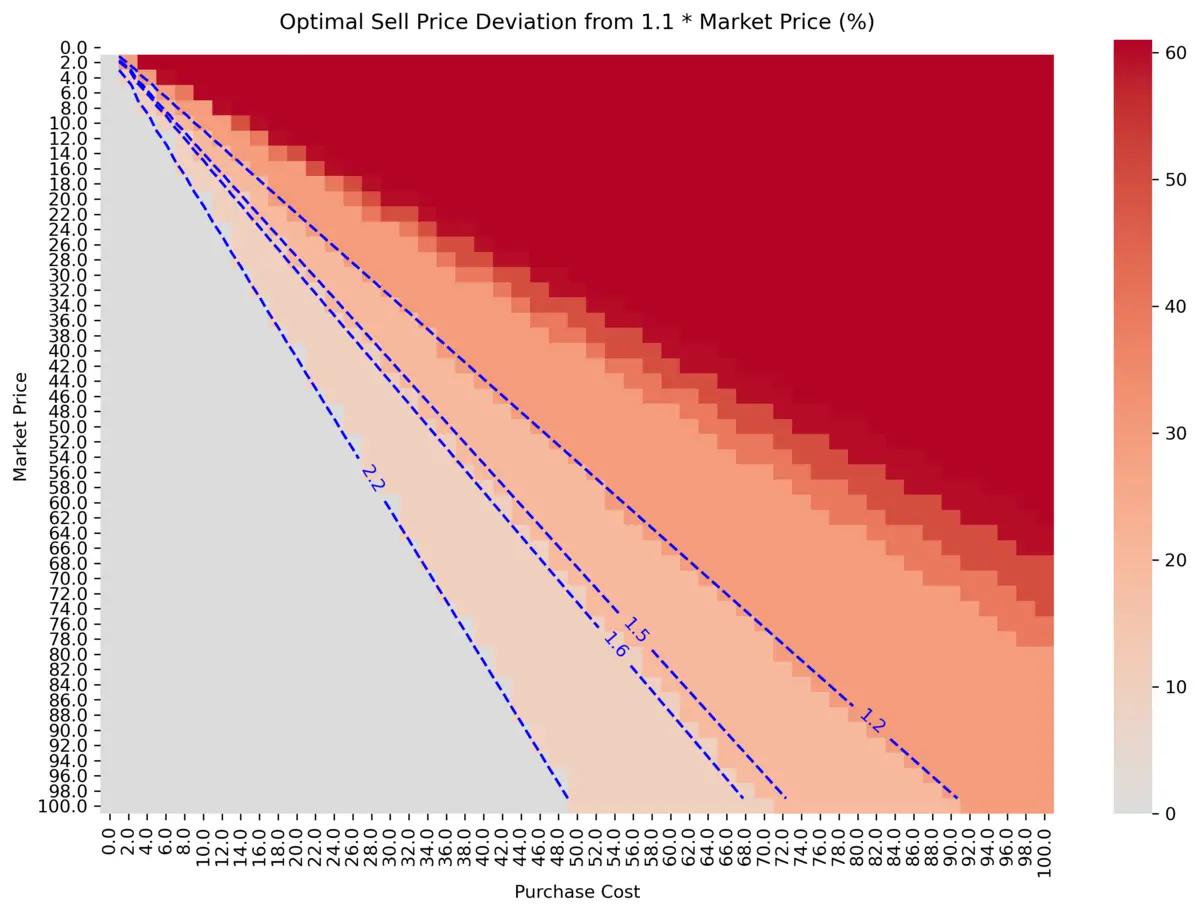
The decision boundary of m_old = 1.4 becomes something between m_new = 1.5 and m_new = 1.6, however m_new = 1.5 is close enough as an approximation for us. With Sell Price = 1.1 * Market Price and m_new = 1.5, the second decision boundary becomes:

1.5 < m = (Profit / Purchase Cost) + 1

0.5 < Profit / Purchase Cost 

0.5 * Purchase Cost < Profit

Purchase Cost < 2 * Profit 

The third decision boundary with Sell Price = Market Price becomes:

1.1 < m = (Profit / Purchase Cost) + 1  

0.1 < Profit / Purchase Cost

0.1 * Purchase Cost < Profit

Purchase Cost < 10 * Profit 

Based on the reformulated decision boundaries, the recommended workflow to determine the optimal Sell Price is:

1. Click on Market Price
2. Compare Profit and Avg Cost
3. If Profit > Avg Cost -> done
4. optional : If 10 * Profit < Avg Cost -> +30% and done
5. If Profit < Avg Cost -> +10% and compare Profit and Avg Cost again
6. If 2 * Profit > Avg Cost -> done
7. If 2 * Profit < Avg Cost -> +10% again (total +20%) and done

Even though theoretically possible, it is very unlikely that 10 * Profit < Avg Cost. It could be that the game does not even allow Market Price and Avg Cost to be this close together. Therefore, step 4 could be skipped, if we do not care for +30% and only consider the options: Market Price, +10% and +20%. Additionally, if we also do not care about +20% and only want to consider Market Price/+10%, than the workflow reduces again to:

1. Click on Market Price
2. Compare Profit and Avg Cost
3. If Profit > Avg Cost -> done
4. If Profit < Avg Cost -> +10% and done

Side note: +20%/+30% markup is not the same as clicking +10% 2 or 3 times in game. However, this is an approximation, that we are willing to make for convenience. This assumes:

• 1.1^2 = 1.21 ~ 1.2
• 1.1^3 = 1.331 ~ 1.3

The deviation is 1% of the Market Price between +20% markup and clicking +10% twice and 3.1% of the Market Price between +30% markup and clicking +10% 3 times.

Credit: @dotalversager